Exercices
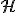 est l'hyperbole d'équation
est l'hyperbole d'équation 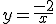 et A est le point de
et A est le point de 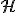 d'abscisse
d'abscisse  non nul.
non nul.
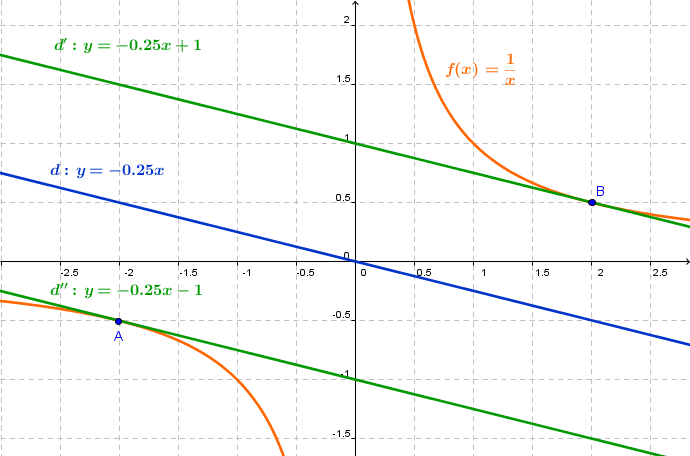
Démontrer que la tangente 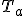 en A a pour équation:
en A a pour équation: 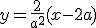 .
.
Tracer 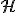 ,
, 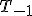 et
et 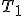 . Pouvait-on prévoir ce résultat?
. Pouvait-on prévoir ce résultat?
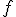 est la fonction inverse. On note
est la fonction inverse. On note 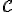 sa courbe représentative.
sa courbe représentative.
a. Existe-t-il des tangentes à 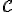 parallèles à la droite d'équation
parallèles à la droite d'équation 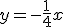 ?
?
b. Existe-t-il des tangentes à 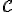 passant par l'origine O du repère?
passant par l'origine O du repère?
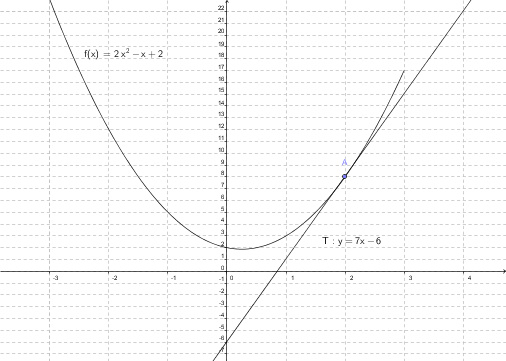
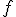 est la fonction définie sur
est la fonction définie sur 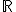 par
par 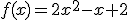 . On appelle
. On appelle 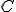 sa courbe représentative dans un repère.
sa courbe représentative dans un repère.
a. Pour tout 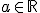 , déterminer
, déterminer 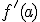 .
.
b. Déterminer l'équation réduite de la
tangente
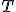 à
à 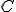 , au point d'abscisse 2.
, au point d'abscisse 2.
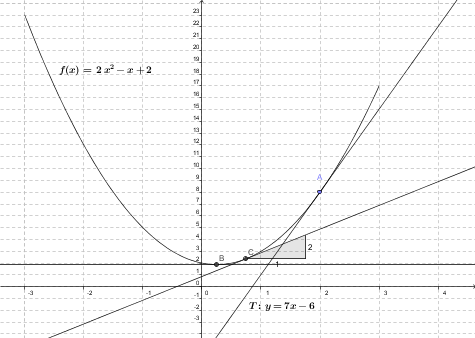
c. Tracer la portion de courbe de 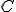 sur l'intervalle [-3 ;3] dans un repère
adapté ainsi que la tangente
sur l'intervalle [-3 ;3] dans un repère
adapté ainsi que la tangente 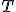 .
.
d. Déterminer les coordonnées du point S de
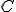 où
la tangente
où
la tangente 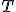 à
à 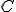 est horizontale.
est horizontale.
e. Existe-t-il un ou des points de 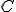 où
la tangente à
où
la tangente à 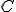 est
parallèle à la droite d'équation y=2x+1
? Préciser ses ou leurs
coordonnées.
est
parallèle à la droite d'équation y=2x+1
? Préciser ses ou leurs
coordonnées.
f. Compléter votre figure avec les réponses aux questions e et f.
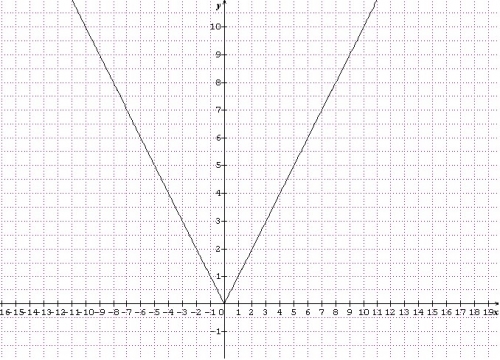
Il existe des fonctions non dérivables en un point. Par exemple, si il y a un point anguleux (c'est le cas de la fonction valeur absolue en 0) ou si la courbe possède une tangente verticale (c'est le cas de la fonction racine carrée).
Démontrer que les fonctions 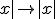 et
et 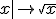 ne sont pas dérivables en 0 et dérivables en toute autre valeur de leur domaine de définition.
ne sont pas dérivables en 0 et dérivables en toute autre valeur de leur domaine de définition.
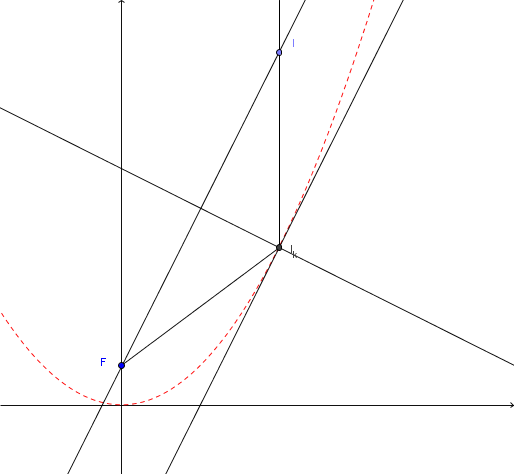
On remarque que les paraboles de télévision ou solaires, (il faudrait d'ailleurs dire paraboloïdes) possèdent un point particulier appelé foyer. Les ondes et les rayons solaires s'y concentrent. Ceux-ci venant de très loin (presque de l'infini), on peut les supposer parallèles.
Pour démontrer le phénomène, prenons la parabole de référence 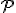 d'équation
d'équation 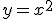 . Considérons les droites verticales
. Considérons les droites verticales 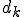 d'équation
d'équation 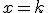 avec
avec 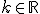 . Chaque droite
. Chaque droite 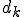 coupe la parabole en un point
coupe la parabole en un point 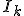 . Considérons maintenant les droites
. Considérons maintenant les droites 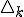 , symétriques des droites
, symétriques des droites 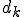 par la réflexion d'axe la tangente à la parabole en
par la réflexion d'axe la tangente à la parabole en 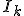 .
.
On veut montrer que les droites 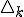 sont concourantes en un même point
sont concourantes en un même point 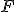 , appelé le foyer de la parabole.
, appelé le foyer de la parabole.
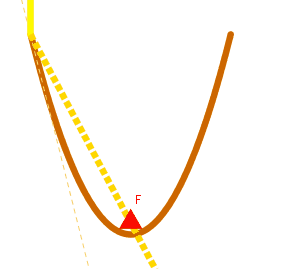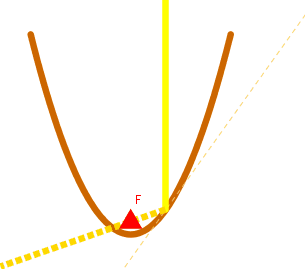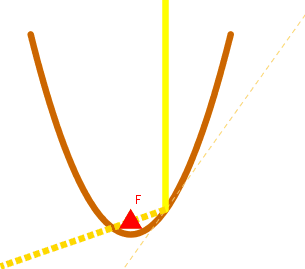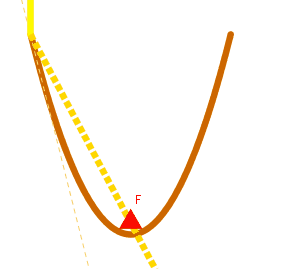
a. En choisissant deux "rayons" particuliers et intéressants, déterminer les coordonnées de 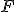 .
.
b. Déterminer l'équation réduite de la tangente à la parabole en 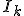 et de la parallèle à cette tangente pasant par
et de la parallèle à cette tangente pasant par 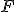 .
.
c. Déterminer les coordonnées 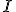 du point d'intersection de cette dernière droite avec la droite
du point d'intersection de cette dernière droite avec la droite 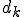 .
.
d. Montrer que le triangle 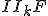 est isocèle en
est isocèle en 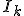 .
.
e. Conclure.
On a tracé les deux paraboles ci-après. 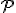 est la parabole orientée vers le haut et
est la parabole orientée vers le haut et 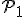 , celle orientée vers le bas. Leur équation respectives sont de la forme
, celle orientée vers le bas. Leur équation respectives sont de la forme 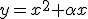 et
et 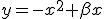 .
.
On définit deux points 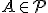 et
et 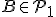 de même abscisse
de même abscisse  .
.
On définit 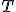 , la tangente à
, la tangente à 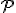 en
en 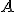 et
et 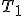 , la tangente à
, la tangente à 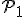 en
en 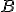 .
.
Montrer qu'il existe une unique valeur de  pour laquelles ces tangentes sont parallèles.
pour laquelles ces tangentes sont parallèles.
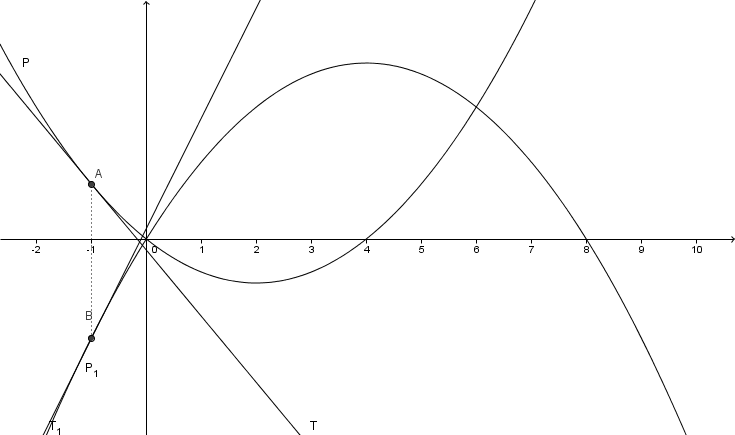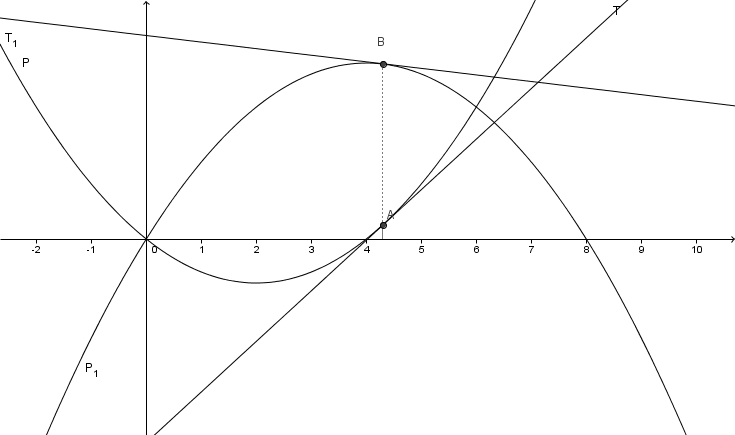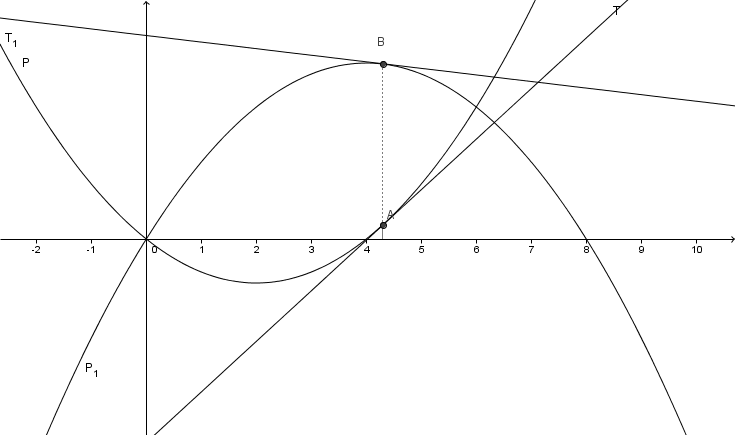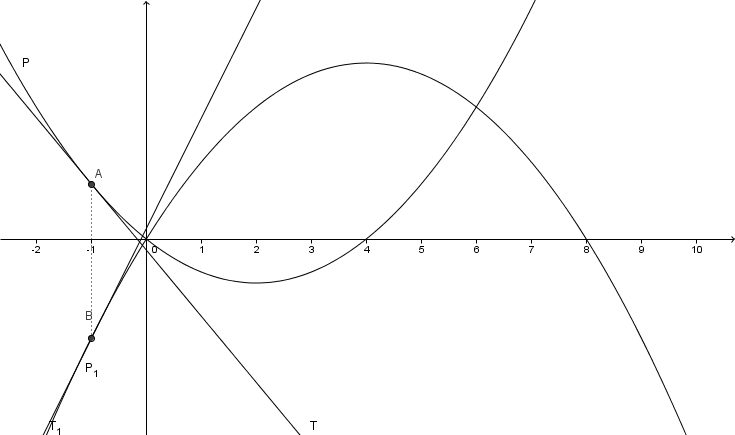
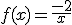 définie sur
définie sur 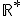
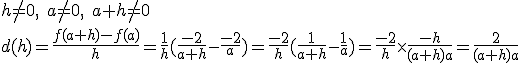
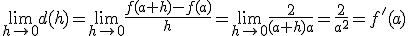
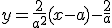
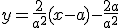 et donc
et donc 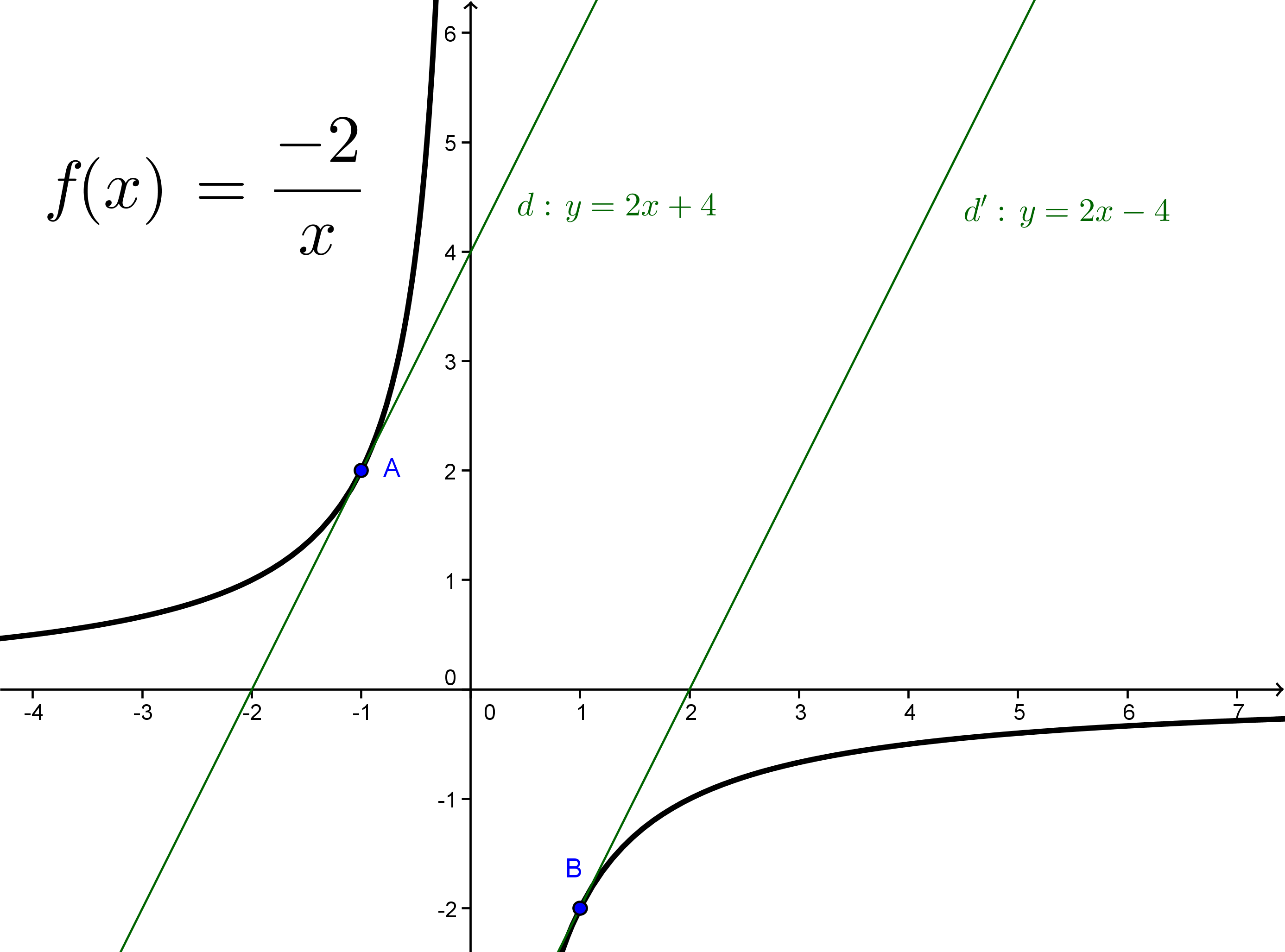
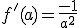 .
.
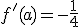 soit
soit 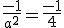 et donc
et donc 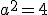 .
.
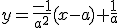 .
.
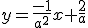 .
.
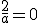 .
.
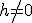 ,
,
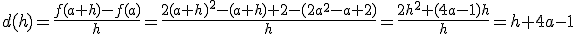
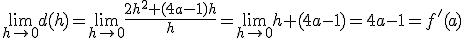
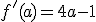
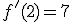 .
.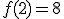
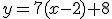
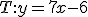
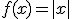 définie sur
définie sur 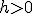
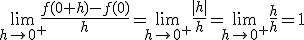 car
car 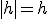
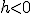
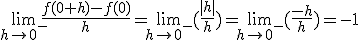 car
car 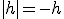
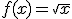 définie sur
définie sur 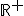 .
.
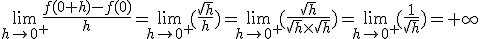
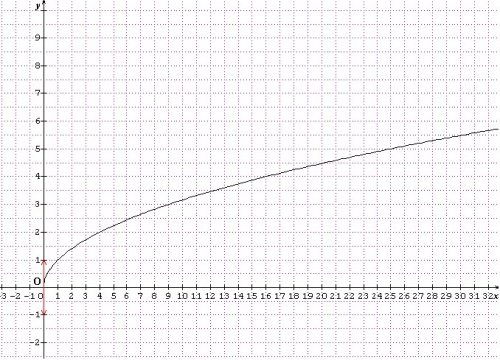
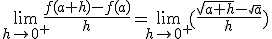
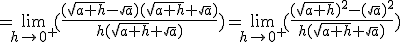
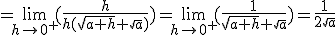
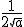 . Ainsi la fonction racine carrée est dérivable sur
. Ainsi la fonction racine carrée est dérivable sur 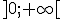 .
.
 a.
a.
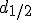 est la droite horizontale passant par
est la droite horizontale passant par 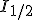 dont l'ordonnée est 1/4.
dont l'ordonnée est 1/4.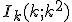 :
:
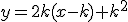 soit
soit 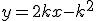
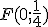 :
:
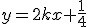
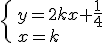
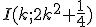 .
.
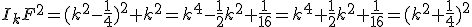
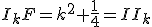
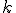 .
.
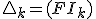 , passent donc par
, passent donc par 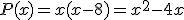
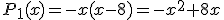
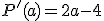
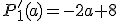
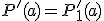 (deux droites parallèles ont des coefficients directeurs égaux), on trouve
(deux droites parallèles ont des coefficients directeurs égaux), on trouve 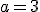 . Ce qui est cohérent avec le graphique.
. Ce qui est cohérent avec le graphique.